6 Publication Bias (Funnel Plot)

Based on Sterne and Egger (2001), the recommended choice for the y-axis is the standard error (in decreasing order) and this is also the default for the funnel() function in the metafor package. In the absence of publication bias and heterogeneity, one would then expect to see the points forming a funnel shape, with the majority of the points falling inside of the pseudo-confidence region with bounds is the estimated effect or outcome based on an equal-effects model and is the standard error value from the y-axis.

### draw funnel plots
funnel(res, main="Standard Error")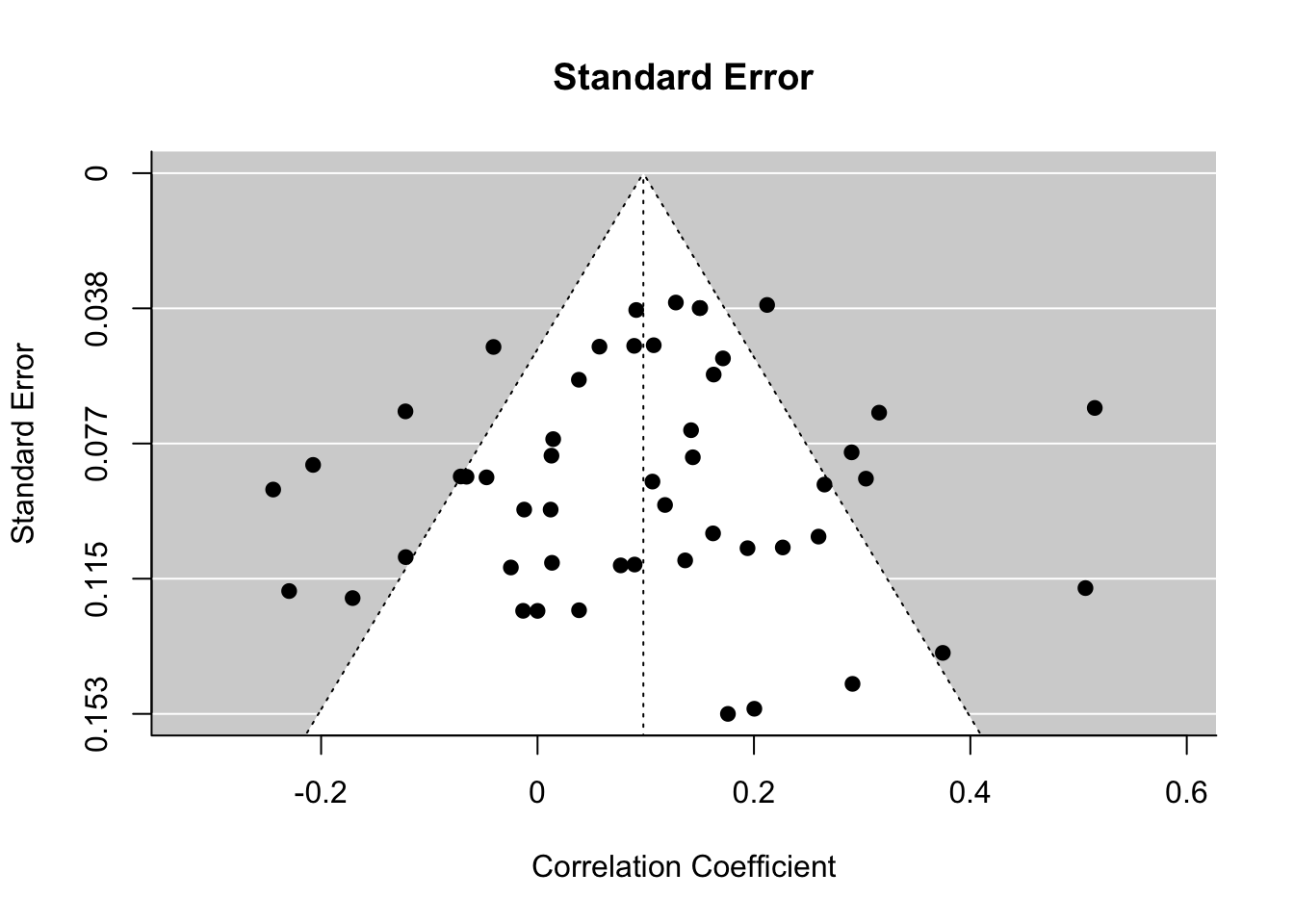

6.1 Egger Test

The Egger test is a test of the relationship between the standard error and the outcome (effect size). While it isn’t a direct test of publication bias, one would hope that the standard error (i.e. the inverse of the sample size) is unrelated to the size of the outcome. If such a relationship is present, then this usually implies asymmetry in the funnel plot, which in turn may be an indication of publication bias

### random/mixed-effects version of the Egger test
regtest(res)

## 
## Regression Test for Funnel Plot Asymmetry
## 
## Model:     mixed-effects meta-regression model
## Predictor: standard error
## 
## Test for Funnel Plot Asymmetry: z = -0.3318, p = 0.7400
## Limit Estimate (as sei -> 0):   b = 0.1183 (CI: -0.0105, 0.2470)